第7回目は、効率的に学習を行う「誤差逆伝搬法(Backpropagation)」について紹介します。
ディープラーニングの基礎の第6回で説明している「勾配法」について、単純な勾配法は実装が簡単であるものの、計算コストが高いという問題があります。
一般的にニューラルネットワーク、ディープラーニング(Deep Learning:深層学習)の学習といえば、この誤差逆伝搬法によるものを指します。損失関数の勾配を求め、より誤差が小さくなる方向に重みパラメータを順次更新するという考え方は勾配法と同じです。勾配を求める際に各重みパラメータごとの偏微分を計算しますが、その偏微分の計算を効率良く行うことができるのが誤差逆伝搬法です。
以下に、計算グラフを用いて誤差逆伝搬法を説明します。
計算グラフ
図1の非常にシンプルな構成のニューラルネットワークを例に説明します。説明を簡略化するために活性化関数などを省略すると、出力層の出力値は、y=(x1×w1+x2×w2)×w3で計算できます。
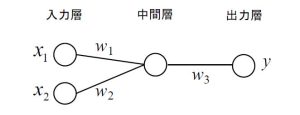
図1 シンプルな構成のニューラルネットワーク
この計算を計算グラフにしたものが図2です。左から右にデータが流れ、計算が進みます。これを順伝搬といいます。
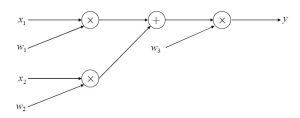
図2 計算グラフ
偏微分の計算
誤差逆伝搬法では、正解値と予測値の誤差をこの計算グラフの出力側から逆方向に伝搬していきます。
y=(x1×w1+x2×w2)×w3 = t×w3とすると、w1についての偏微分は次式の通り分解できます。実際には、yと正解値との間の誤差を損失関数L(w)で評価することになるので、損失関数L(w)を偏微分することになります。
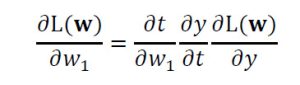
w2についての偏微分も同様です。
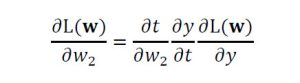
この偏微分を計算グラフと対応付けると図3、図4となります。出力層に近い偏微分の計算結果
は、重みパラメータw1、w2それぞれについての偏微分の計算で共通であり、毎回計算する必要はないことが分かります。このように出力層から順に入力層に向けて偏微分を計算し、計算済みの結果を伝搬することで効率良く入力層に近い重みパラメータの偏微分を計算していく手法が、誤差逆伝搬法です。
今回の例は、極めてシンプルなネットワークのためあまりメリットがあるようには感じないかもしれませんが、ディープラーニングではネットワークが多層となり、かつ非常に多くの重みパラメータが存在するため、有用な手法です。
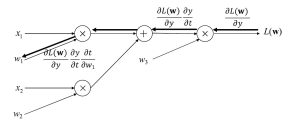
図3 計算グラフにおける重みパラメータw1についての偏微分の計算
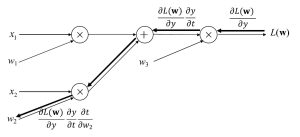
図4 計算グラフにおける重みパラメータw2についての偏微分の計算
ここでは、説明を簡略化するために活性化関数などの説明は省略しました。活性化関数が加わっても基本的な考え方は同じです。誤差逆伝搬法の基本原理だけでも理解しておくと、ディープラーニングがどのようにものごとを学習しているのかが分かってきます。ニューラルネットワーク、ディープラーニングの研究、設計、開発で役立つはずです。
次回は「コンピュータビジョン」について、応用事例の紹介も交えながらまずその概要を説明します！